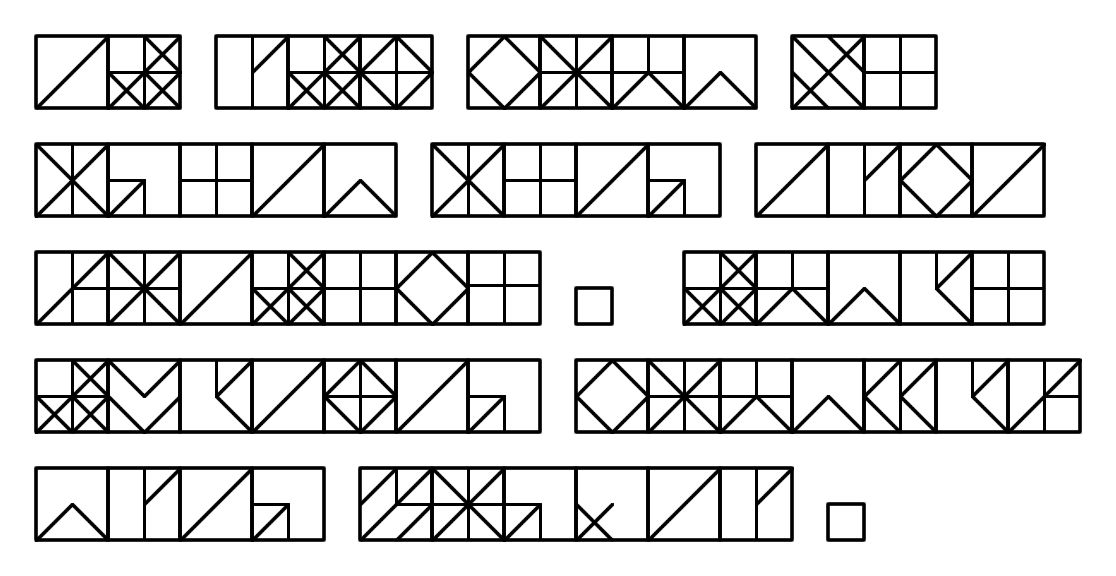
Tag 22: Das ist das Haus vom Nikolaus
Verfasst: 21.12.2024, 20:27
von Zarunias
In diesem Thread kann das folgende Rätsel diskutiert werden:
Tag 22: Das ist das Haus vom Nikolaus
Erstellt von: Zarunias
Bitte während der Rätselzeit keine Tipps oder gar die Lösung öffentlich posten. Posts werden in diesem Fall zensiert. Nach Einsendeschluss darf ohne Einschränkungen diskutiert werden.
Auflösung
Tag 22: Das ist das Haus vom Nikolaus
Erstellt von: Zarunias
Bitte während der Rätselzeit keine Tipps oder gar die Lösung öffentlich posten. Posts werden in diesem Fall zensiert. Nach Einsendeschluss darf ohne Einschränkungen diskutiert werden.
Auflösung
Lösung: DBEHFEIGHDGACIFC
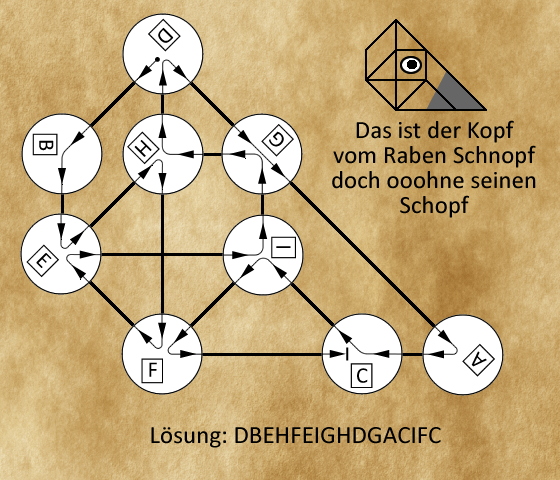
Hier ein ausführlicher Lösungsweg. (Das ist jetzt nur ein Beispiel - es gibt sicherlich auch viele andere Möglichkeiten, um zur Lösung zu kommen. Eine offensichtlich sehr beliebte Alternative war Mit-den-Teilen-herumspielen-und-Glück-haben.)
Man kann mit ein paar logischen Schlüssen anfangen:
Am interessantesten ist sicherlich der "Rand" der Figur (erstmal ignorieren wir die Pfeilrichtungen, und die genauen Verbindungen innerhalb der einzelnen Teilen).
Wenn man den ganzen Rand der Figur abgehen will, muss man zwangsweise einmal im Kreis gehen, man kommt ja schließlich zum Ausgangspunkt zurück. Während dieser Wanderung muss man sich dabei einmal komplett um die eigene Achse drehen. Das sind 360°

Jetzt schauen wir uns die einzelnen Teile an, und was für eine Drehung sie uns erlauben würden; dazu schaut man sich einfach den größten Winkel an:
A; 135° bzw. 3 Achteldrehungen
B: 45° bzw. 1 Achteldrehung
C: 0°
D: 90° bzw. 2 Achteldrehungen (zur Erinnerung: die Pfeilrichtung ignorieren wir erstmal - und auch, dass die Pfade hier nicht zusammenhängen)
E: 45° bzw. 1 Achteldrehung
F: 45° bzw 1 Achteldrehung
G: 0°
H: -45° bzw eine negative Achteldrehung - Wenn dieses Teil am Rand liegt, drehen wir uns also wieder zurück.
I: -45° bzw eine negative Achteldrehung
Wenn wir den Rand der Figur abgehen, müssen wir uns ja insgesamt 360° drehen. Mit den vorhandenen Teilen geht das nur, wenn wir alle positiven Drehungen nehmen, und alle negativen vermeiden.
Man kann also schlussfolgern, dass A,B,D,E,F am Rand der Figur, und H und I im Inneren liegen müssen.
Als nächsten Schritt kann man sich die Pfeilrichtungen anschauen (immer noch am Rand der Figur):
von A,B, D, E und F führen insgesamt 6 Pfeile weg, und nur 4 Pfeile hin (wenn man nur die Randpfeile zählt). Damit man einen gültigen Rand bilden könnte müssten diese Zahlen aber gleich sein. Daraus folgt, dass auch C am Rand sein muss.
Es ist jetzt also nur noch bei G ungewiss, ob das am Rand liegt.
Am Rand hat man aufgrund der Pfeile noch 2 generelle Möglichkeiten:
Entweder hat man am Rand im Uhrzeigersinn D-C-F-E, wobei A, B zwingend, und optional auch G noch irgendwo dazwischen eingeschoben werden.
Oder man hat im Uhrzeigersinn D-E-F-C, auch hier müssen A und B, und optional auch G noch eingeschoben werden.
Diese Möglichkeiten kann man ab hier eigentlich schon durchprobieren, um in vernünftiger Zeit die Lösung zu finden..
Man kann aber noch einen weiteren logischen Schritt machen. Vom Startteil D weg läuft man ja jeden Pfad genau einmal entlang. Hier kann man zusammenzählen, wie oft man sich dabei in jede Richtung dreht, bis man beim Endteil C ist (3 Achteldrehungen gegen den Uhrzeigersinn bzw. 5 im Uhrzeigersinn). Damit wird die relative Drehung zwischen C und D eindeutig bestimmt. Der zweite Fall oben lässt sich somit ausschließen, außerdem muss A zwischen D und C sein.
Damit bleiben für den Rand (im Uhrzeigersinn gesehen) nur noch 2 Möglichkeiten:
Entweder D-A-C-F-E-B (optional noch G zwischen D-A, zwischen A-C oder zwischen F-E)
oder D-A-C-B-F-E (auch hier optional noch G zwischen D-A, zwischen A-C oder zwischen F-E)
Und diese beiden Möglichkeiten sind jetzt tatsächlich sehr schnell kontrollierbar.

Hier ein ausführlicher Lösungsweg. (Das ist jetzt nur ein Beispiel - es gibt sicherlich auch viele andere Möglichkeiten, um zur Lösung zu kommen. Eine offensichtlich sehr beliebte Alternative war Mit-den-Teilen-herumspielen-und-Glück-haben.)
Man kann mit ein paar logischen Schlüssen anfangen:
Am interessantesten ist sicherlich der "Rand" der Figur (erstmal ignorieren wir die Pfeilrichtungen, und die genauen Verbindungen innerhalb der einzelnen Teilen).
Wenn man den ganzen Rand der Figur abgehen will, muss man zwangsweise einmal im Kreis gehen, man kommt ja schließlich zum Ausgangspunkt zurück. Während dieser Wanderung muss man sich dabei einmal komplett um die eigene Achse drehen. Das sind 360°

Jetzt schauen wir uns die einzelnen Teile an, und was für eine Drehung sie uns erlauben würden; dazu schaut man sich einfach den größten Winkel an:
A; 135° bzw. 3 Achteldrehungen
B: 45° bzw. 1 Achteldrehung
C: 0°
D: 90° bzw. 2 Achteldrehungen (zur Erinnerung: die Pfeilrichtung ignorieren wir erstmal - und auch, dass die Pfade hier nicht zusammenhängen)
E: 45° bzw. 1 Achteldrehung
F: 45° bzw 1 Achteldrehung
G: 0°
H: -45° bzw eine negative Achteldrehung - Wenn dieses Teil am Rand liegt, drehen wir uns also wieder zurück.
I: -45° bzw eine negative Achteldrehung
Wenn wir den Rand der Figur abgehen, müssen wir uns ja insgesamt 360° drehen. Mit den vorhandenen Teilen geht das nur, wenn wir alle positiven Drehungen nehmen, und alle negativen vermeiden.
Man kann also schlussfolgern, dass A,B,D,E,F am Rand der Figur, und H und I im Inneren liegen müssen.
Als nächsten Schritt kann man sich die Pfeilrichtungen anschauen (immer noch am Rand der Figur):
von A,B, D, E und F führen insgesamt 6 Pfeile weg, und nur 4 Pfeile hin (wenn man nur die Randpfeile zählt). Damit man einen gültigen Rand bilden könnte müssten diese Zahlen aber gleich sein. Daraus folgt, dass auch C am Rand sein muss.
Es ist jetzt also nur noch bei G ungewiss, ob das am Rand liegt.
Am Rand hat man aufgrund der Pfeile noch 2 generelle Möglichkeiten:
Entweder hat man am Rand im Uhrzeigersinn D-C-F-E, wobei A, B zwingend, und optional auch G noch irgendwo dazwischen eingeschoben werden.
Oder man hat im Uhrzeigersinn D-E-F-C, auch hier müssen A und B, und optional auch G noch eingeschoben werden.
Diese Möglichkeiten kann man ab hier eigentlich schon durchprobieren, um in vernünftiger Zeit die Lösung zu finden..
Man kann aber noch einen weiteren logischen Schritt machen. Vom Startteil D weg läuft man ja jeden Pfad genau einmal entlang. Hier kann man zusammenzählen, wie oft man sich dabei in jede Richtung dreht, bis man beim Endteil C ist (3 Achteldrehungen gegen den Uhrzeigersinn bzw. 5 im Uhrzeigersinn). Damit wird die relative Drehung zwischen C und D eindeutig bestimmt. Der zweite Fall oben lässt sich somit ausschließen, außerdem muss A zwischen D und C sein.
Damit bleiben für den Rand (im Uhrzeigersinn gesehen) nur noch 2 Möglichkeiten:
Entweder D-A-C-F-E-B (optional noch G zwischen D-A, zwischen A-C oder zwischen F-E)
oder D-A-C-B-F-E (auch hier optional noch G zwischen D-A, zwischen A-C oder zwischen F-E)
Und diese beiden Möglichkeiten sind jetzt tatsächlich sehr schnell kontrollierbar.